一、前言

对于数据存储结构常见有：数组、单链表、双线链表、二叉树、多叉数、哈希表、红黑树等，其中红黑树可以自平衡二叉查找树,对于这几种数据结构的遍历查询速度性能，对比效率由小到大：O(1)<O(lgn)<O(n)< O(nlgn)<O(n2)< O(n3)<O(2n)<O(n!)<O(nn)（如下图,lgn对数）。

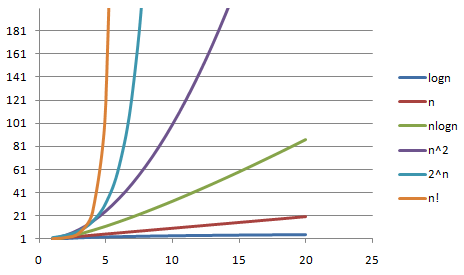
数组普通遍历=O(n)@b@数组二分查找遍历=二叉树=红黑树=O(lg2n)@b@多叉数=O(lgn)@b@哈希表=数组+红黑树/链表=HashMap=HashSet=O(nlgn)@b@数组两层嵌套遍历（两个for循环）=O(n2)@b@数组三层嵌套遍历（三个for循环）=O(n3)

二、集合对比

1.List - 序列（有序的集合，可重复）

ArrayList -> 数组 ->O(n)@b@    --get() 直接读取第几个下标，复杂度 O(1)@b@    --add(E) 添加元素，直接在后面添加，复杂度O（1）@b@    --add(index, E) 添加元素，在第几个元素后面插入，后面的元素需要向后移动，复杂度O（n）@b@    --remove（）删除元素，后面的元素需要逐个移动，复杂度O（n）@b@LinkedList ->链表@b@    --get() 获取第几个元素，依次遍历，复杂度O(n)@b@    --add(E) 添加到末尾，复杂度O(1)@b@    --add(index, E) 添加第几个元素后，需要先查找到第几个元素，直接指针指向操作，复杂度O(n)@b@    --remove（）删除元素，直接指针指向操作，复杂度O(1) @b@@b@对比分析：ArrayList 查询快，新增删除慢，LinkedList 相反@b@Vector --线程安全的ArrayList

2.Set-类集（不同类别集合，不可重复）

HashSet -> HashMap -> 数组++红黑树/链表->O(nlgn)@b@--不有顺序大小类集@b@TreeSet->二叉树->O(lg2n)@b@--有大小顺序、可排序的类集

3.Map-键值关系存储

HashMap->数组+红黑树/链表->O(nlgn)@b@--无插入顺序,非线程安全，根据HashCode决定存放数组位置@b@LinkedHashMap->数组+双向链表->O(nlgn)@b@--最近读取的数据放在最前面，最早读取的数据放在最后面，从而实现LRU缓存机制（最近最少使用）@b@TreeMap->红-黑二叉树->O(log n)@b@--默认键值的升序排序,非线程安全@b@注：Hashtable - 基于Dictionary类实现，线程安全，HashMap是其简单实现

三、时间复杂度 - 即 T(n) = O(f(n))

1、常数阶O(1)  -  无论代码执行了多少行，只要是没有循环等复杂结构（即使有几万几十万行），那这个代码的时间复杂度就都是O(1)，如：

int i = 1;@b@int j = 2;@b@++i;@b@j++;@b@int m = i + j;

2、线性阶O(n)  - for循环里面的代码会执行n遍，因此它消耗的时间是随着n的变化而变化的，这类代码都可以用O(n)来表示

for(i=1; i<=n; ++i)@b@{@b@   j = i;@b@   j++;@b@}

3、对数阶O(logN) - 在while循环里面，每次都将 i 乘以 2，乘完之后，i 距离 n 就越来越近，也就是说 2 的 x 次方等于 n，那么 x = log2^n

int i = 1;@b@while(i<n)@b@{@b@    i = i * 2;@b@}

4、线性对数阶O(nlogN) - 将时间复杂度为O(logn)的代码循环N遍的话，那么它的时间复杂度就是 n * O(logN)

for(m=1; m<n; m++)@b@{@b@    i = 1;@b@    while(i<n)@b@    {@b@        i = i * 2;@b@    }@b@}

5、平方阶O(n²) - 把 O(n) 的代码再嵌套循环一遍，复杂度就是 O(n*n)，即 O(n²)

for(x=1; i<=m; x++)@b@{@b@   for(i=1; i<=n; i++)@b@    {@b@       j = i;@b@       j++;@b@    }@b@}

6、立方阶O(n³) - 上面的O(n²) 去理解就好了，O(n³)相当于三层n循环